aGraph

Function plotter with some analysis.

aGraph bei Google Play

Home Deutsch Български

FEAUTURES:

Draw functions and derivatives.
Present working area as curve, area below curve oder rotationbody
Colors can be freely configured
Many settings and options
Integrated help
Screenshot
Detailed HTML Reporting
Function value table
Move the axes via touch
Move the margins via touch
Multitouch zoom in/zoom out
App Links:
As example https://graph.tchekov.net/app/FX=SIN(DIV(X,CST(2)))

Starts the application with F(x) = sin(x/2)

https://graph.tchekov.net/app/FX=SIN(DIV(X,CST(2)));GX=COS(X) etc.
Calculations with curves:

Find roots with regula falsi and Brent
Length
Point of gravity

Calculations with areas (between funktion und x-axis, or between both functions)

Numerical integration (Simpson 's rule)
Point of gravity
Inertia

Calculations with rotationbody

Volume
Lateral surface
Point of gravity
Inertia

USAGE:

Symbol	Function
	Opens the main 'menu'
	Create screenshot
	Open the function settings. Scroll up/down to find the needed setting and tap on it. According to the selection, appropriate change methode will be offered. Also opens the settings for 'Work with - Build from'.
	Here you switch visibility of view elements such as derivatives, grid, calculation result etc. To toggle visibility just tap on item.
	Set the root finding method used with the touch-and-move margin functionality.
	Creates and shows different reports (such as: full function value table, application log, report) in html format. If the storage permission is granted the report will be also saved. Report creation takes some time, if needed respective progress bar will be shown for this period.
	Opens the color settings pane.
	Opens the dimension settings pane.
	Show current calculation results. Here you can copy calculation result for further usage. It is also possible here to create detailed report for the calculations.

LICENSE:
aGraph is Freeware.
aGraph is called in the following software.

LIMITED WARRANTY:
THIS SOFTWARE IS PROVIDED 'AS-IS' AND WITHOUT WARRANTY OF ANY KIND, EXPRESS, IMPLIED OR OTHERWISE, INCLUDING WITHOUT LIMITATION, ANY WARRANTY OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE.
IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR ANY SPECIAL, INCIDENTAL, INDIRECT OR CONSEQUENTIAL DAMAGES OF ANY KIND, OR ANY DAMAGES WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER OR NOT ADVISED OF THE POSSIBILITY OF DAMAGE, AND ON ANY THEORY OF LIABILITY, ARISING OUT OF OR IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE, EXCEPT TO THE EXTENT OF ANY UNAVOIDABLE STATUTARY LIABILITY.

USE AND DISTRIBUTION OF THIS SOFTWARE IS FREE:
YOU ARE HEREBY LICENSED TO MAKE AS MANY COPIES OF THIS SOFTWARE AS YOU WISH; GIVE EXACT COPIES OF THE ORIGINAL VERSION TO ANYONE; AND DISTRIBUTE IN ITS UNMODIFIED FORM VIA ELECTRONIC MEANS. THERE IS NO CHARGE FOR ANY OF THE ABOVE. YOU ARE AUTHORIZED TO FREELY USE THIS SOFTWARE.

Mathematical backgrounds

PGraph uses two approximation methods which I will try to describe. For deep-going information, please look into all good mathematics books.

This text serves only as extension for the PGraph operating instructions, other purposes arenot intended.

Regula Falsi

The so called "Wrong rule" (or Secant Method) is a procedure for determination of intersections (method for solving equations of finding roots).

We look for the x - value, that makes F(x) to 0 (intersection of F(x) and the x - Axis).

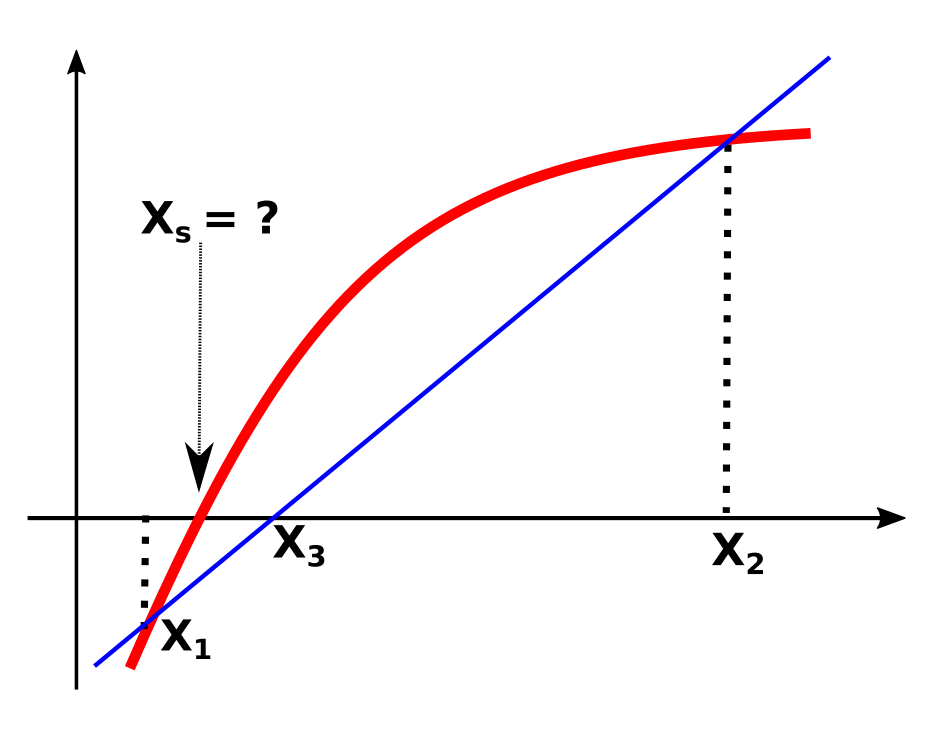
F(x) is replaced by the secant, so the formula:

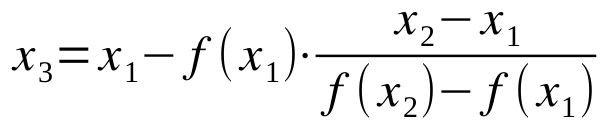
supplies us an approximate value (the intersection of the secant with the x axis).

If we repeat this procedures often enough with values X₁ and X₃ or X₂ and X₃ (aGraph makes this 100 times, or until F(X₁)=F(X₂)) - we will become an value that is very close to the real one. The approximation is sufficient for ordinary purposes, mathematical is it however NOT correct. These procedure functions only if some basic conditions are given - for further information please look into the appropriate books.

aGraph example: We look for the 1. solution of the equation sin(x)=1/x-1. So we input for f(x) sin(x) and for g(x) 1/x-1. First we want to take a look over these Functions, then we should click somewhat left from the 1. Intersection (the 1. Solution) and take the value (about 0.5...) for the lower bound. For upper limit you can input 1 (we can also draw the function one more time, so we were able to click this time right from the intersection and receive a value for the upper limit).

Simpson's Rule (Numeric integration)

The procedures for numeric determination of surface under function (integration) are based on the same basic principle: The surface must be divided into many strips, finding the surface or every single strip, and then sum of all strips.

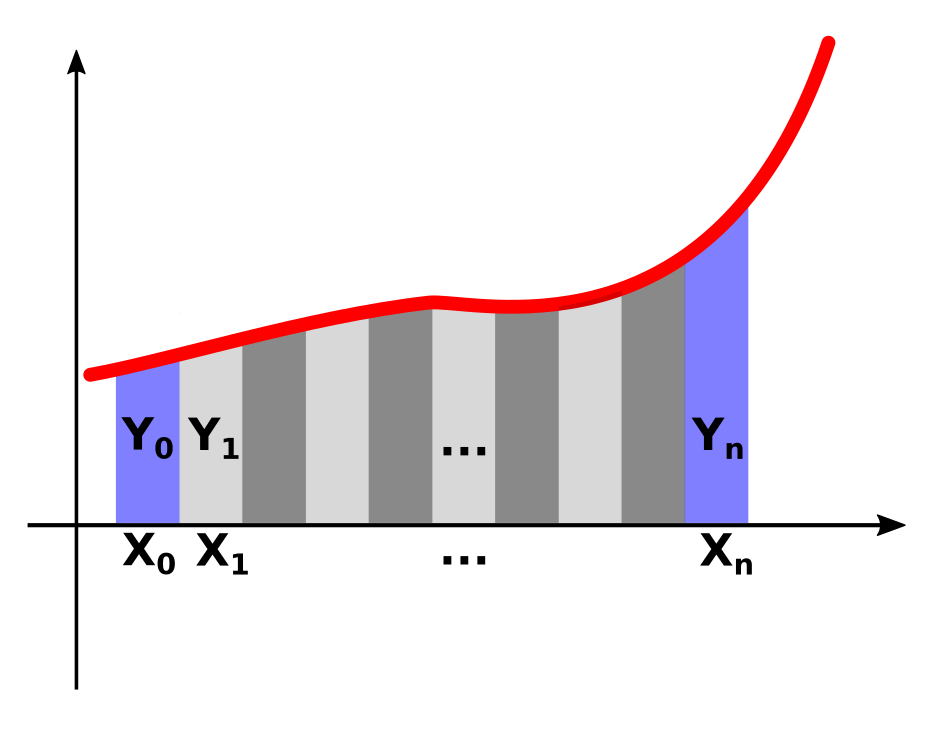
The Simpson procedure uses parabola as upper delimitation of the stripes (other procedures use straight lines).

This supplies better approximate values. To define a parabola we needs at least 3 points, also Simpson Method uses double strips.

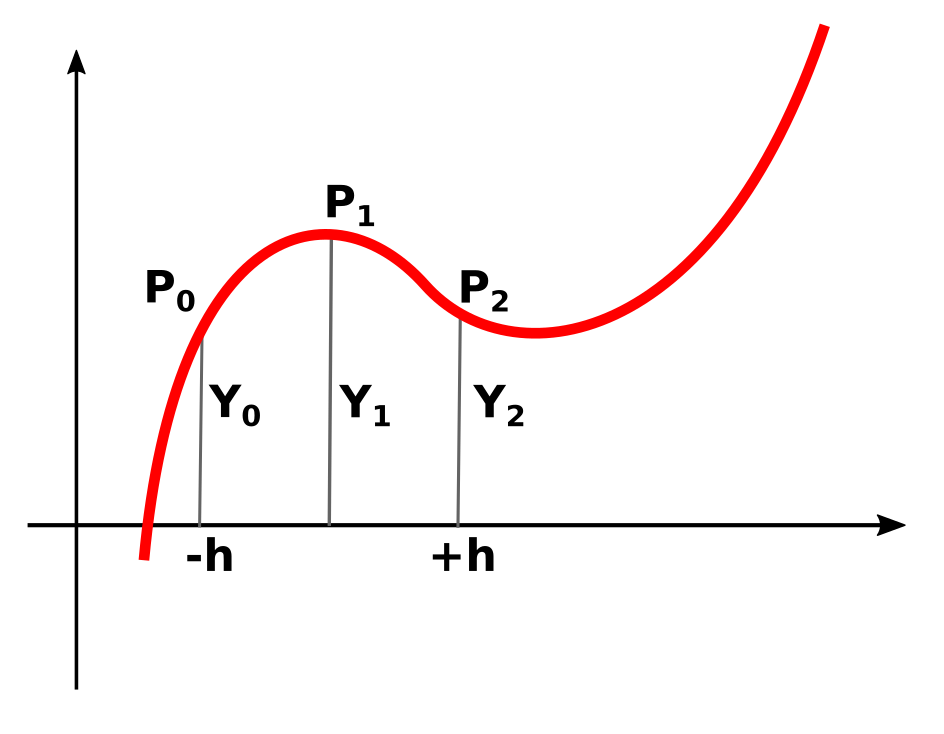
First the surface is divided at even number of stripes (PGraph - uses 100), then find the strip width h.

Double stripes P₀, P₁, P₂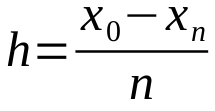
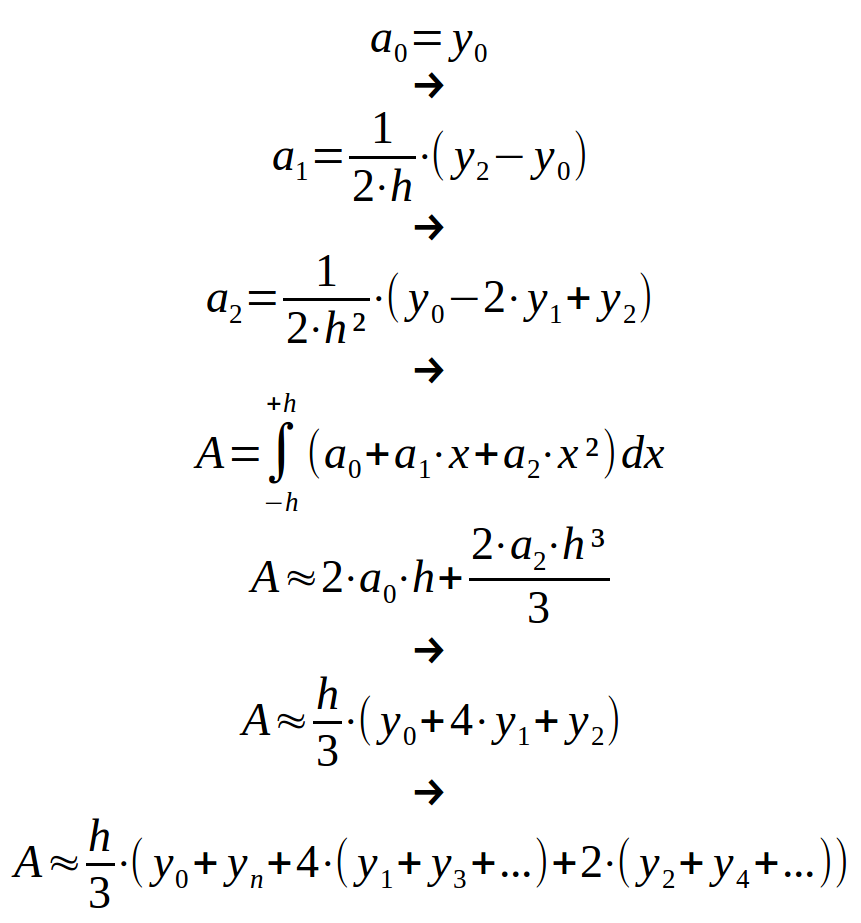
Single stripe width:

Number of stripes n
Coordinates:
P₀ (-h, Y₀),
P₁ (0, Y₁),
P₂ (+h, Y₂)
Parabola formula: Y = a₀ + a₁x + a₂x² =>
Y₀ = a₀ - a₁h - a₂h²
Y₁ = a₁
Y₂ = a₀ + a₁x + a₂x²

Afterwards the three sums are created (Summ1 = first + last strips, Summ2 = sum of the odd strips, Summ3 = sum of the even strips).

Then the last formula is used and we receives a numeric approximate value for the surface under the function.

Example in aGraph: How big is the surface between the functions sqrt(1 x^2) and sqrt(1 x^2)?
First we must shift the functions into the upper quadrants, otherwise we will get we falsified values (there is visibly a surface present, but we will become 0). So we must take 1+sqrt(1 x^2) and 1-sqrt(1-x^2) instead. Thus both functions stand above the x axis. It is easy to recognize that we have a circle with r=1, so the lower limit is -1, upper limit is 1, the surface is equal to a natural constant ...

All further abilities of aGraph, which are based on integration, develop on the Simpson procedure.

Data security policy:

aGraph does not collect any data. Nothing is collected, transfered, saved or analysed.

aGraph will ask only for "Write external storage" permission which is neede is you wish to save your reports

The application will work just fine withot this permission, only the reports you create will be temporary and will not be saved.